Structured and Interpretation of Computer Programs

2nd edition - Harold Abelson, Gerald Jay Sussman and Julie Sussman

1. Building Abstractions with Procedures

Concepto o idea sobre los procesos computacionales.- entes abstractos que pueden llegar a manipular datos y cuya evolución es orientada por un conjunto de reglas y patrones, llamado programa.

Los procesos computacionales están cuidadosamente compuestos de expresiones y lenguajes de programación esotericos que prescriben las tareas que tienen que realizar los procesos.

Los sistemas computacionales bien diseñados, al igual que un reactor nuclear o un automóvil, están diseñados modularmente. Esto permite que las partes puedan ser construidas, reemplazadas y depuradas por separado.

Programming in Lisp

Para describir los procesos y expresar el pensamiento procedural humano, el libro utiliza el lenguaje Lisp (LISt Processsing). Lenguaje que fue concebido por John McCarthy, como un formalismo que permitiese razonar sobre expresiones lógicas llamadas recursion equations y symbolic algebra, por lo que incluyó nuevos tipos de datos como listas y átomos.

Debido a su flexibilidad y elegancia, Lisp fue evolucionando y dando lugar a nuevos dialectos del lenguaje, por lo que actualmente, más que un lenguaje, es una familia de dialectos dentro de los cuales está Scheme, el lenguaje que se utilizará a lo largo del libro.

Si bien Lisp no es de los lenguajes más eficientes ni actuales, posee ciertas características que lo hacen único y excelente para la enseñanza de los conceptos relacionados con la programación y las estructuras de datos. Una de las peculiaridades de Lisp, es la capacidad de poder representar y manipular procedures (descripción de procesos) como datos Lisp, esto lo hace ideal para escribir programas que deben manipular otros programas como datos, como los intérpretes y compiladores.

1.1 The Elements of Programming

Un lenguaje de programación ofrece 2 tipos de elementos con los cuales tratar (aunque no son realmente tan distintos):

1. Datos : lo que se desea manipular.
2. Procedimientos : descripción de reglas para la manipulación de los datos.

Todo lenguaje eficaz ofrece 3 mecanismos para combinar simples ideas y formar otras más complejas:

1. Expresiones primitivas
2. Medios de combinación
3. Medios de abstracción

1.1.1 Expressions

Las expresiones que representan números, por ejemplo, pueden ser combinados con expresiones que representan un procedimiento primitivo (+ o *) para formar expresiones que representan el resultado de la aplicación de tales procedimientos:

(+ 153 147)
(- 512 100)
(* 5 99)
(/ 5 2)

→ 300
→ 412
→ 495
→ 2.5

• Los paréntesis denotan la aplicación del procedimiento y son llamados combinaciones.
• A la convención de ubicar el operador a la izquierda de los operandos se le conoce como prefix-notation o también notación polaca.

La notación prefija tiene muchas ventajas, desde las claridad hasta el anidamiento convencional:

(+ 32 51 93 9)
(+ (* 3 (+ (* 2 4) (+ 3 5))) (+ (- 10 7) 6))

(+ (* 3
      (+ (* 2 4)
         (+ 3 5)))
   (+ (- 10 7)
       6))

→ 185
→ 57
→ 57

• Las dos últimas combinaciones producen el mismo resultado, con la diferencia de que el último tiene un formato conocido como pretty-printing.
• Al proceso del intérprete de leer, evaluar e imprimir el resultado también se le conoce como read-eval-print loop.

1.1.2 Naming and the Environment

En Scheme las variables (nombre que referencia a un objeto computacional) se definen mediante define.

(define pi 3.14159)
(define radius 10)
(define circumference (* 2 pi radius))

circumference

→ 62.8318

• Define es el medio de abstracción más simple del lenguaje que permite la creación de estructuras más complejas y fomenta un desarrollo y testeo incrementales.
• Los pares nombre:objeto (variables), son almacenados en una especie de memoria denominada global environment o entorno global, que en ocasiones, puede involucrar un número diferente de entornos.

1.1.3 Evaluating Combinations

El intérprete para realizar la evaluación de combinaciones, realiza lo siguiente:

1. Evalúa las subexpresiones de la combinación.
2. Aplicar el procedimiento situado al extremo izquierdo (operador) a los argumentos que son los operandos.

Se puede ver que, en el primer paso, para lograr la evaluación de la combinación, primero se debe realizar la evaluación de cada elemento de la combinación, por lo que su propia regla de evaluar, forma parte de su primera etapa de evaluación, es decir, la evaluación es de naturaleza recursiva.

Por ejemplo, si se quisiera evaluar la siguiente combinación, este requeriría que la regla de evaluación sea aplicada a las cuatro diferentes combinaciones.

(* (+ 2 (* 4 6)) (+ 3 5 7))

Una visualización más gráfica es la de representar la combinación en forma de árbol, donde los nodos terminales van filtrándose hacia arriba, formando otras combinaciones hasta, finalmente, obtener el resultado. A este tipo de proceso se le conoce como tree accumulation o acumulación de árbol.

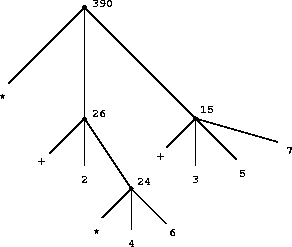
Fig 1.1: Representación en árbol mostrando el valor de cada subcombinación.

Para la evaluación de los casos primitivos se establece que:

• Los valores numéricos, son los números que estos representan.
• Los valores de lo operadores incorporados son instrucciones máquina que llevan a cabo la operación que representan.
• Los valores de otros nombres, son los objetos asociados con esos nombres en el entorno.

Los símbolos como + y *, también estan incorporados en el entorno global y es el entorno el encargado en determinar el significado de los símbolos en las expresiones, es decir, el entorno provee un contexto en el que tiene lugar la evaluación.

Existen excepciones a la regla general de evaluación como define x 3, ya que los argumentos x y 3 no son una combinación, sino un proceso de asignación. A casos excepcionales como este, se le conoce como special forms o formas especiales donde define es un ejemplo de special form y tiene su propia regla de evaluación.

• A diferencia de otros lenguajes, Lisp tiene una sintáxis bastante simple y uniforme donde la regla general de evaluación puede ser descrita junto a un pequeño conjunto de reglas especializadas para un número de formas especiales.
• El syntactic sugar es una forma “conveniente” de crear construcciones sintácticas que hacen del lenguaje menos uniforme y que en palabras de Alan Perlis: “El azúcar sintáctico causa cáncer de punto y coma”.

1.1.4 Compound Procedures

Todo lenguaje de programación eficaz debe de implementar los siguientes elementos:

• Los números y las operaciones aritméticas son datos y procedimientos primitivos.
• El anidamiento de combinaciones provee un medio para combinar operaciones.
• Las definiciones que asocian nombres con valores proveen un limitado medio de abstracción.

A continuación se tratará sobre una técnica de abstracción que permite nombrar una operación compuesta y referenciarlo como una unidad, denominado compound procedure:

(define (<name> <formal parameters>) <body>)

• <name>: símbolo que asocia la definición del procedimiento en el entorno.
• <formal parameters: nombres usados dentro del cuerpo del procedimiento para referenciar a los argumentos del prcedimiento.
• <body>: secuencia de expresiones que producirán el valor del procedimiento cuando los parámetros se reemplacen por los argumentos requeridos.

Creando un compound procedure que permite elevar un número x al cuadrado:

(define (square x) (* x x))
(define (sum-of-squares x y) (+ (square x) (square y)))
(define (f a) (sum-of-squares(+ a 1) (* a 2)))

• Al igual que con los procedimientos primitivos, es posible realizar combinaciones para formar otras más complejas con los procedimientos compuestos.

1.1.5 The Substitution Model for Procedure Application

Para evaluar una combinación que involucra un procedimiento compuesto, el intérprete aplica el mismo proceso que para combinaciones con procedimientos primitivos.

El modelo de sustitución para la aplicación de procedimientos que se describe a continuación ayuda a pensar sobre la aplicación del procedimiento, mas no es una descripción de como funciona el intérprete.

(f 5)
(sum-of-squares (+ a 1) (* a 2))
(sum-of-squares (+ 5 1) (* 5 2))
(+ (square 6) (square 10))
(+ (* 6 6) (* 10 10))
(+ 36 100)

→ 136

• De hecho, la “sustitución” se realiza mediante el uso de un entorno local para los parámetros formales.
• Existen diferentes modelos mucho más complejos de como funciona el intérprete (el modelo de sustitución es el primero de ellos para empezar a pensar formalmente sobre el proceso de evaluación).

Applicative order versus normal order

En el proceso de evaluación de combinaciones que realiza el intérprete, este primero evalúa el operador y los operandos para luego aplicar el procedimiento resultante (sección 1.1.3); pero este no es la única manera de realizar la evaluación.

Método de evaluación normal-order evaluation o “expandir todo y luego reducir”:

(f 5)
(sum-of-squares (+ 5 1) (* 5 2))
(+ (square (+ 5 1)) (square (* 5 2)))
(+ (* (+ 5 1) (+ 5 1)) (* (* 5 2) (* 5 2)))

(+ (* 6 6) (* 10 10))
(+ 36 100)

→ 136 

• Si bien este método y el aplicative-order evaluation o “evaluar los argumentos y luego aplicar” que actualmente usa el intérprete, pueden llegar al mismo resultado con valores legítimos, en algunos casos sus resultados pueden diferir.
• Lisp utiliza la evaluación de orden aplicativo debido a la eficiencia frente a expresiones repetidas como (+ 5 1), y además por que el otro método, normal-order evaluation, se vuelve complejo en modelos diferentes al de sustitución.

1.1.6 Conditional Expressions and Predicates

Uso de case analysis para calcular el valor absoluto de un número:

      ┌
      |  r   if r > 0
|r| = |  0   if r = 0
      | -r   if r < 0
      └

Para representar un análisis de caso se utiliza cond de “condicional”:

(define (abs x)
  (cond ((> x 0) x)
        ((= x 0) 0)
        ((< x 0) (- x))))

(define (abs x)
 (cond ((< x 0) (- x))
       (else x)))

• El símbolo - utilizado con un solo operando indica negación.
• En Scheme, cualquier otro valor diferente de false (#f) es verdadero (#t).
• También se puede utilizar else al final de cond.
• Al valor que se evalua (true/false), se le denomina predicado.
• También se le conoce como predicado al procedimiento que retorna true/false.

Condicional restringido solo a dos casos de análisis:

(define (abs x)
    (if (< x 0)
          (- X)
            x))

• La forma general de if es: (if <predicate> <consequent> <alternative>).
• La pequeña diferencia entre cond e if, es que este último solo acepta expresiones simples en <consequent> y <alternative>.

Además de predicados primitivos como >, <, >= o <= hay operaciones de composición lógica que permiten realizar predicados compuestos:

(and <e1> ... <en>)
(or  <e1> ... <en>)
(not <e1>)

• Mencionar que and y or son formas especiales, no procedimientos; ya que no se evalúan todas las subexpresiones, a diferencia de not que si es un procedimiento ordinario.
• La evaluación de las expresiones es de izquierda a derecha.

Ejemplos:

(define (>= x y)
    (and (> x y) (= x y)))

(define (>= x y)
    (not (< x y)))

• Ambas definiciones son iguales.

Ejemplo de la grandiosa flexibilidad de Scheme:

(define (a-plus-abs-b a b)
        ((if (> b 0) + -) a b))

• Dependiendo de si el valor de b es mayor a menor a 0, if retorna un operador primitivo (+ o -), más precisamente, un procedimiento primitivo que recibe como argumentos la a y la b con los cuales operar.

1.1.7 Example: Square Roots by Newton’s Method

La forma común de calcular la raíz cuadrada de un número, es mediante el método de Newton, que permite obtener el resultado a partir de aproximaciones sucesivas, ejemplo:

Guess           Quotient            Average
1               2 / 1 = 2           (2 + 1) / 2 = 1.5
1.5             2 / 1.5 = 1.333     (1.333 + 1.5) / 2 = 1.4167
1.4167          2 / 1.4167 = 1.4118 (1.4167 + 1.4118) / 2 = 1.4142
1.4142          ...                 ...

• Mientras más se continúe con la secuencia, se obtiene un mejor resultado.

2. Building Abstractions with Data

3. Modularity, Objects, and State

4. Metalinguistic Abstraction

5. Computing with Register Machines